Cosine similarity 1D convolutions
Sign and scale independent 1D convolutions with cosine similarity
The cosine similarity function below provides sign and scale independent 1D convolutions. It has a learnable parameter $p$ where large values of $p$ increase the sharpness of the cosine similarity. Here $u$ is the signal and $v$ is the kernel (e.g. $[1,2,3]$).
$$\text{CosineSim}(u,v)=\text{sign}(u \cdot v)\text{abs}(\frac{u \cdot v}{|u|_2 \cdot |v|_2})^{p^2}$$
We consider the kernel $[1,2,3]$ and a 1D time series signal with 5 distinct motifs:
- A. exact match $[1,2,3]$
- B. negative sign, exact match $[-1,-2,-3]$
- C. downscaled exact match $[0.2, 0.4, 0.6]$
- D. median $[2,2,2]$
- E. reversed $[3,2,1]$
We can compare a 1D convolution with kernel_size=3, dilation = 1, and padding = (kernel_size-1)*dilation = 2 against the cosine similarity distance.
1D convolution correctly gives the largest activation to both of the exact matches (A and B). However, the convolution also gives a large activation to parts of the signal where there should not be a match. The median sequence of values B $[2,2,2]$ and the reversed sequence E $[3,2,1]$ get a significantly high activation despite having no similarity to the filter. The downscaled exact match C is not selected by the convolution because of the scale of the filter. Standard convolutions on raw (unnormalized) data are not scale and sign independent. Common normalizations, like batch or layer norm, calculates normalizing terms over samples or channels but not point-wise. The resulting convolved signal requires max pooling to find the subsequences of greatest correlation with the filter.
In contrast, the cosine similarity gives a score of 1 or -1 only for exact matches. The feature is detected independent of sign or scale. The figure below shows that the cosine similarity distance correctly detects the motifs A, B, and C. If we set the sharpness parameter to an arbitratily large value $p=9$ then the only points are the exact matches.
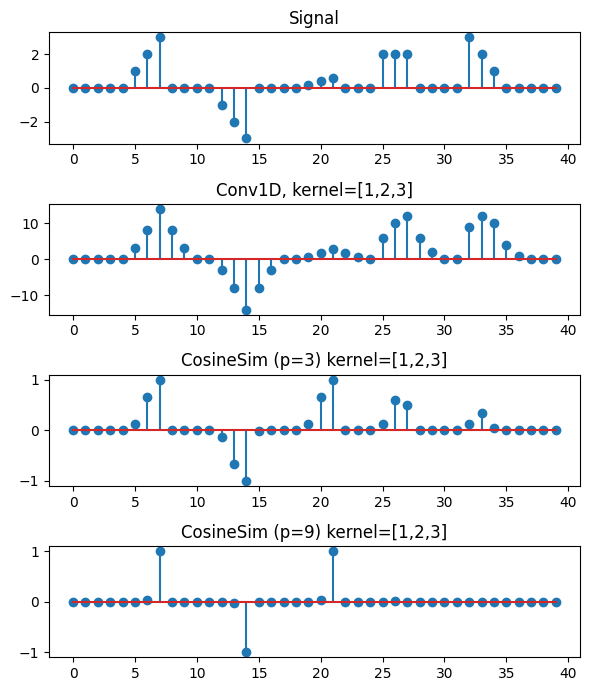
The output of CosineSim is clearly interpreted as the points of maximal correlation between the signal susequence and the filter, where filters represent subsequence templates.
def cosine_similarity(signal, kernel, sharpness, padding):
"""
Compute the cosine similarity distance between a signal and a kernel.
Outputs a sequence of the same length as the signal.
Parameters
----------
signal : torch.Tensor
input [batch_size, channels, length]
kernel : torch.Tensor
filter [kernel_size]
sharpness : float
sharpness parameter
padding : int
padding size, (kernel size-1) * dilation
Returns
-------
torch.Tensor
output [batch_size, channels, length]
"""
kernel_size = kernel.size(-1)
x = F.pad(signal, (padding,padding))
x = x.unfold(2, kernel_size, 1)
sim = F.cosine_similarity(x, kernel, dim=-1)
sgn = torch.sign(torch.einsum('bdij,k->bdi', x, kernel))
sim = sgn * torch.pow(torch.abs(sim), (sharpness**2))
sim = sim[:, :, : -padding].contiguous()
return sim